Machine Learning -- Neural Network

There's an ever increasing amount of excitement in the industry surrounding Neural Networks, which seems to create a race to figure out various ways of using them. This is great, I love AI, and Neural Networks are not new, actually I believe the concept dates back to the '80s. However, I'm starting to notice a disturbing trend that a Neural Network is being treated as a magical solution, the excitement seems to be creating hordes of documentation that fail to describe what a Neural Network is and only seeks to show how to use one for a specific problem. Thus, I'm accelerating my personal schedule and writing this quick high level intro to try and fill in the gaps I'm noticing in documents/tutorials out there.

I'll try to keep this really high level and talk about concepts, and the desires behind each step of the process. Thus I hope everyone that reads this will be able to remove a bit of the mystery surrounding Neural Networks. As everything having to do with Machine Learning, any serious discussion must start with math. The reason why we start there, is that's all a Neural Network can do, it is limited and empowered by the rules of math. Thus, let's dig into some very basic math. The most to start with is to define a function.

What's a function?

A function is a way to relate some input to an output. This is to say, all functions within math will take some number of inputs and create exactly one output that corresponds to those inputs. A property of a function is every time it has exactly the same input, it will yield the same output every time. Also note that what is output, doesn't have to be just one number, it could be a structure like a vector or matrix.

Now given those rules, quite a large number of surprising things can be thought of as a function. That's the reason why computer programs can do so many things, they're just running some math function (a fact that creates a great deal of debate around patent law). In any case, the main thing I want to drive home is a function can be as complex or as simple as we want to make it. It can be linear: `y = f(x) = x + 1` it could be parabolic: `y = f(x) = x^2 + 1` or take many inputs: `y = f(a,b,c,d) = 23 * a + 42 * b + 51 * c + d` or could provide a gradient descent from linear regression: `\frac{\partial}{\partial\thetaj} \frac{1}{2m}\sum_{i=1}^m((\theta_0 + \theta_1*x_i) + y_i)^2`. It can even do things that we can't even describe:

Find Diagnosis = f(symptoms) = Some unknown function?

Here we're talking about a function that might not even exist, but if there is a function that can relate the inputs of a patients symptoms to the outputs of a diagnosis, then the function that we don't even know how to write is denoted here, and what we're looking for.

As I mentioned in linear regression, Machine Learning seeks to simply find a function that best fits the data; Neural Networks are a type of machine learning, and are kind of one of the most generic tools in our arsenal for finding unknown functions. However, the limitation of it being very generic means that while it will find a function, it might not be the best implementation to use; however, more on that later.

Learning from Nature:

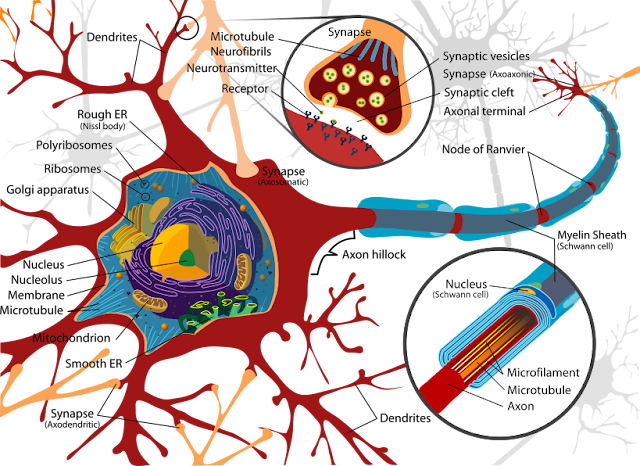
Let's take some inspiration from how the human brain works. This is exciting stuff to talk about. The entirety of all human thought works from a very simple principal. From the principals that govern evolution, cells formed a remarkable ability in specialization. Some cells evolved to have a structure which provides the ability to take input from other cells and decide to "fire" or not. Let's deeply look at how this process happens in nature:

The neurons that make the entire system work are three parts. The ability to take input from other neurons, Dendrites, those are the spidery web structure, for our purposes, they provide input. The next major thing to highlight is the output from the neuron, Axons, That's the long tube at the back of the neuron that has the Axon Hillock attachment to the neuron cell and terminates at the Axon Terminal. The Synapse, is the gap between one neuron's Axon Terminal and another neuron's Dendrite. Now looking at all of that, please notice the awesome fact that each Neuron has a LOT of Dendrites (inputs) and one source of Axon (outputs). Remember that math function definition? That's exactly what's happening here; the actual logical process between inputs and outputs happens within the cell when it "decides" to activate or not; thus the rest of the neuron cell is the third major part, or the Cell Body.

Now we're not entirely sure how the Cell Body makes a decision, but we do know that it takes a certain combination of each Dendrite providing input to activate the Axon. To continue down the rabbit hole of what we know about the biological process, all sensory input, eye sight, ears, touch, etc, combined with all commands to the body from muscle movement to recalling memory can be accounted for by this simple process of the Neuron working in concert with trillions of other neurons. Even human memory works by having each neuron working in concert to create a pattern; while some parts of the brain will specialize around tasks those parts perform often, each part can relearn other tasks depending upon need. For more reading check here.

Mimicking nature:

With the above knowledge in mind, we can replicate how the natural brain works. By taking input, making a decision on it and creating output. So our artificial neurons would look something like this if it has 3 inputs and one output:

This means that our artificial neuron has a mathematical function of `output = f(x, y ,z)`. Now up until now, I've left the function that the neuron does on the input as a mystery. It's time to clear that mystery up. Let's try an experiment, assume that the function is a linear one; that is it describes either a straight line or a plane. This means we're assuming the function is `output = f(x, y, z) = constantA * x + constantB * y + constantC *z + constantD`. This means that all constants can be the same or different.

Now in this Neural Network graph, the output comes directly off of N6. So let's look at how the math breaks down:
Final Layer:

• `output = N6_(output)`
• `N6_(output) = ConstantA * N5_(output) + ConstantB * N4_(output) + ConstantC * N3_(output) + ConstantD`

Hidden Layer:

• `N3_(output) = ConstantE * N1_(output) + ConstantF * N2_(output) + ConstantG`
• `N4_(output) = ConstantH * N1_(output) + ConstantI * N2_(output) + ConstantJ`
• `N5_(output) = ConstantK * N1_(output) + ConstantL * N2_(output) + ConstantK`

First Layer:

• `N1_(output) = ConstantM * X + ConstantN * Y + ConstantO * Z + ConstantP`
• `N2_(output) = ConstantQ * X + ConstantR * Y + ConstantS * Z + ConstantT`

Now if we combine all of the above equations, all of our effort will result in being able to reduce it to the following equation:
`output = f(x,y,z) = ConstantA * X + ConstantB * Y + ConstantC * Z + ConstantD` Which means, that our neural network just reduced down to a single linear function. Oops. That happens because a combination of linear functions is ALWAYS linear. No matter how you try to give each node something new, it will only ever result in extra work for the processor that can be reduced to a simpler linear function. That wont do, and we've now eliminated any desire for using linear functions (no matter how intuitive they might be).

Let's try that again with a non-linear function, that is a non-linear function is one that does not have a linear relationship between the inputs and outputs. That solves our issue, and gives us a surprising feature. By the Universal Approximation Theorem any function can be approximated by a neural network of non-linear functions. Think about that for a second, if a function can relate the input and the output, any neural network using a non-linear function can approximate the function that correctly represents input/output.

While many non-linear functions exist, I prefer to start talking about the easiest to grasp and program. Sigmoid functions or `htheta(x) = 1 / (1 + e^(-theta^Tx))` become the "activation function" usually denoted as `g(z)` and provides a known way to create a single neuron. Thinking about why Sigmoid works, you can see that it will never have a value that is not between 0 and 1 or off and on to varying degrees. Thus if the value of the activation function is greater than 0.5 it can be known to activate the output. Well wait, 0.5 is our cutoff? What if we want to allow for us to give each node a bias. Let's adjust our network to look like this:

The way to read that is the output is activated `g(x)` if the input of both X and Y are activated. Let's go through the math so it makes sense: `htheta(x) = g(-30 + 20 * X + 20 * Y)`

X	Y		Output
0	0		`g(-30) approx 0`
1	0		`g(-10) approx 0`
0	1		`g(-10) approx 0`
1	1		`g(10) approx 1`

In the truth table above, we can see that for all of our labor, our single layer Neural Network just built a binary "And" function. Now combining more layers, where each node can feed into another node increases the complexity, time it takes to learn and potentially raises the likelihood that the network will over specialize. However, it's important to note that Neural Networks are incredibly expensive. In my "And" example, if you know the function ahead of time that you're looking for, "And" is always a single op constant function. However, in a neural network, the trained values of -30 -10 -10 must be found over the training set by reducing the distance of the error to the predicted function.

This reduction to the right predicted function can be done with our familiar gradient descent from logistic Regression. Just as with logistic regression, pick weights for each edge and minimize until you arrive at the global optimum for that incarnation of a Neural network implementation.

As each network requires training, it must figure out that the function is an "and" function. This process is VERY expensive. It's far better to use something other than a Neural Network if it's possible to know the relation before hand. However, when you want to find the function, and linear regression, SVD, or other cheaper Machine learning functionality fails to provide your answer, a Neural Network should eventually reduce to the correct function.